伟大的范畴理论
范畴理论是数学上的一种新的语言和框架结构. 对于程序员来说,它是另一种思考方式,一种极度有效的方式来提取规律(Extremely efficient for generalization) Programming is doing Math.编成的工作其实就是数学的工作。
范畴是一种表达事物(things) 和路径(ways) to go between things. 这可以参考thinking like a git,因为他也是一种基于范畴理论, 而延伸出来的实际产物,方便程序员对于development的管理。
A Category C is defined by:
- Objects ob(C),
- Morphisms hom(C),
- a Composition law (∘)
Functor : (ob->ob)
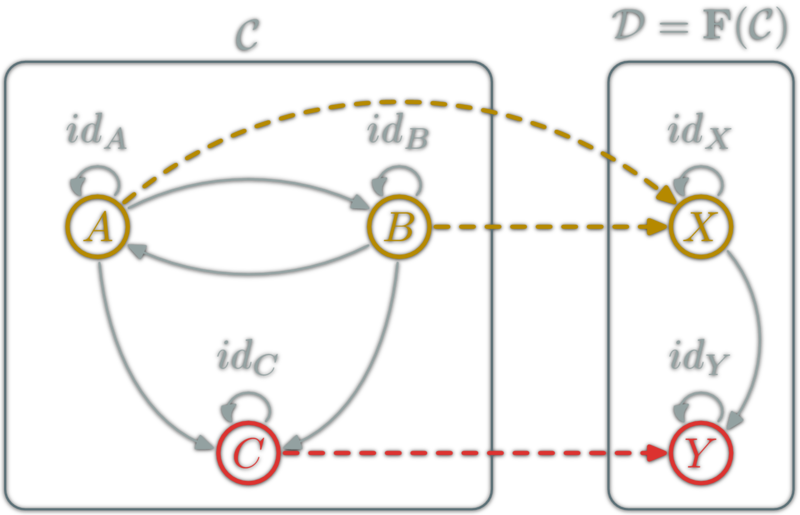
Functor : (hom->hom)
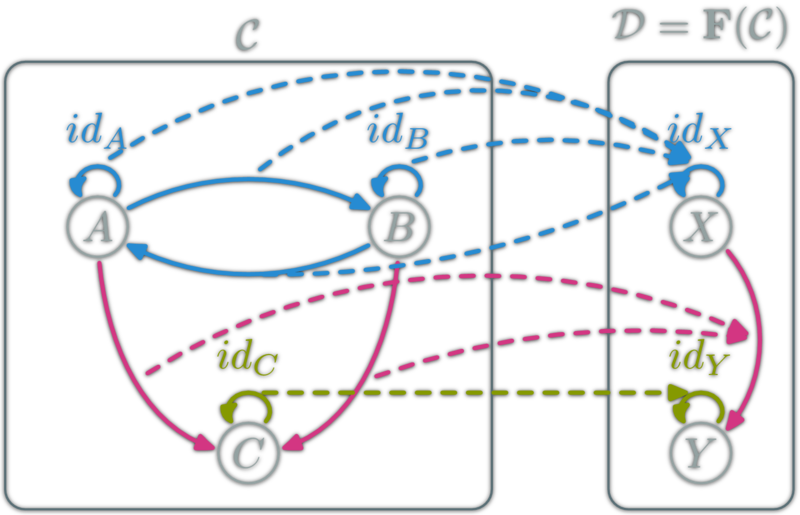
Endofunctors:


Categories and functors form a category: Cat
- ob(Cat) are categories
- hom(Cat) are functors
- ∘ is functor composition
A Haskell Functor is a type F :: * -> * which belong to the type class Functor ; thus instantiate fmap :: (a -> b) -> (F a -> F b).
- F: ob(Hask)→ob(Hask)
- & fmap: hom(Hask)→hom(Hask)
The couple (F,fmap) is a Hask’s functor if for any x :: F a:
fmap id x = x
fmap (f.g) x= (fmap f . fmap g) x