Good Story Makeup Behind

pattern

Be sure you know and understand them better than if we had written each definition for you. The key to programming is recognizing patterns in data and processes. The Commandments Highlight the patterns.

Early in the book, some concepts are narrowed for simplicity; later, they are expanded and qualified.

What should we do with the dots in the second line and the terminate line? (or can you fill the dots in the following definition of two-in-a-row-b?)—->

the actually ideal method for make a theis, make what you wanna do into structural story!(Structural Copy of saying)

(define sum-of-prefix-b_
  (lambda (ss tup)
    (cond
      ((null? tup) ...)
      (else (cons  ... 
                  (sum-of-prefix-b_ ... 
                                    (cdr tup)))))))

What should we do with the dots in the second line and the terminate line? –> which means you know what to do when the special pattern has been hit(when (car lat) is not equal of preceding , or lat is not null)–yeah, you must understand what the functions work!

The trick

Explain precisely what it does! it means function.

Whether continuing the search is useful to find the answer for you! Or not?

We must know the job or meaning for every function, in order to arrange them into structure or pattern.

The trick of two-in-a-row-b? receives two arguments and one tells it something about the other, That is, the first argument, preceding, always occurs just before the second argument, lat, int the original list, while the trick is also applied int the sum-of-prefixs-b and tail recursion method.

(Commandants: Use the additional arguments when a function needs to know what other arguments to the function have been like so far.)

difference

(define sum-of-prefix-b_
  (lambda (ss tup)
    (cond
      ((null? tup) (quote ()))
      (else (cons (+ ss (car tup))
                  (sum-of-prefix-b_ (+ ss (car tup))
                                    (cdr tup)))))))
(define sum-of-prefix_
  (lambda (tup)
    (sum-of-prefix-b_ 0 tup)))


(define sum-of-prefix2_
  (lambda (tup)
    (letrec ((sum-of-prefix-b2_ (lambda (ss tup)
                                  (cond
                                    ((null? tup) (quote ()))
                                    (else (cons (+ ss (car tup))
                                                (sum-of-prefix-b2_ (+ ss (car tup))
                                                                   (cdr tup))))))))
      (sum-of-prefix-b2_ 0 tup))))

(sum-of-prefix2_ '(1 2 3 4 5))


(define sum-of-prefix3_
  (lambda (tup)
    (letrec ((sum-of-prefix-b3_ (lambda (ss tup)
                                  (cond
                                    ((null? tup) (quote ()))
                                    (else
                                     (let ((left_thing (+ ss (car tup))))
                                       (cons left_thing
                                             (sum-of-prefix-b3_ left_thing (cdr tup)))))))))
      (sum-of-prefix-b3_ 0 tup))))


(sum-of-prefix3_ '(1 2 3 4 5))

What is the difference between scramble and sum-of-prefix? We know that scramble takes a non-empty tup in which no number is greater than its own index(要求), and returns a tup of the same length. Eatch number in the argument is treated as a backward index from its own position to a point earliere in the tup. The result at each position is found by counting backward from the current position according to this index. That is,, scramble needs to know that entire prefix of each element so that it can use the first element of tup as a backward index to pick the corresponding number from this prefix(Here subjection or mean to us that the additional function definition for what most of the work for scramble, to collect information about the prefix of each element in the same manner as sum-of-prefixes)

The former needs to know the actual prefix(瞬时值), the latter(sum-of-prefix) needs to know the sum of the numbers in the prefix(特征值)

good story maker

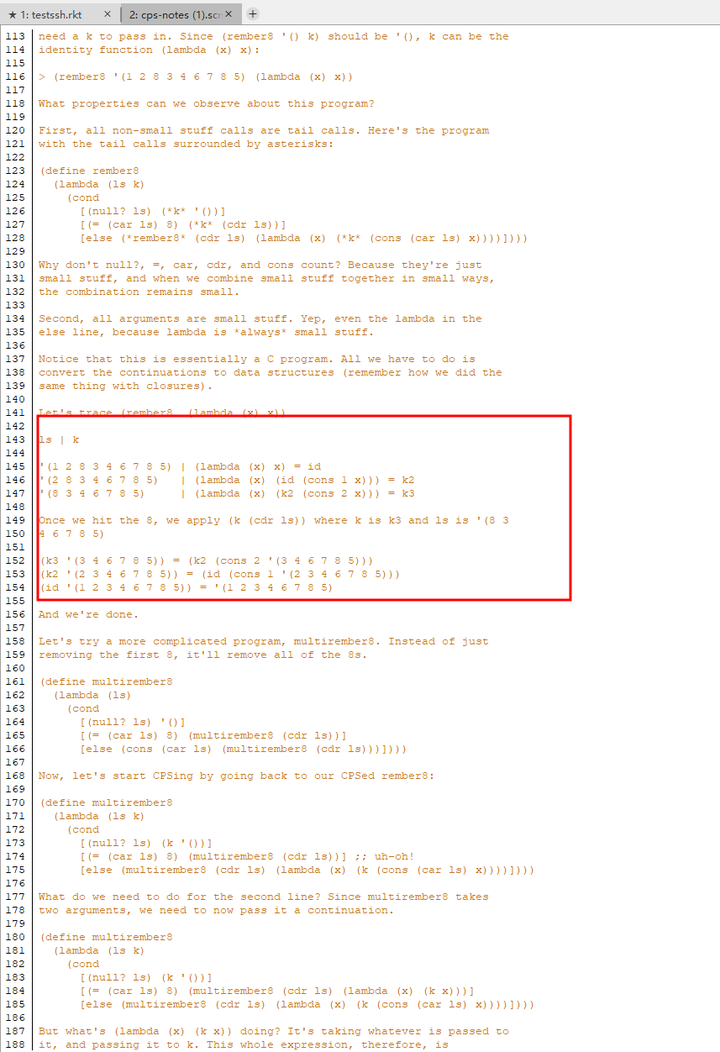
每一个好的故事背后都有好的故事设计者 注意rember8的形式

(define rember8
  (lambda (a lat)
    (cond
      ((null? lat) (quote ()))
      ((eq? (car lat) a) (cdr lat))
      (else (cons (car lat)
                  (rember8 a (cdr lat)))))))

(define rember8b
  (lambda (a lat)
    (letrec ((rem? (lambda (lat)
                     (cond
                       ((null? lat)(quote ()))
                       ((eq? (car lat) a) (cdr lat))
                       (else (cons (car lat)
                                   (rem? a (cdr lat))))))))
      (rem? lat))))

(define rember8k
  (lambda (a lat tail)
    (letrec ((rem? (lambda (lat)
                     (cond
                       ((null? lat)(tail (quote ())))
                       ((eq? (car lat) a) (tail (cdr lat)))
                       (else (rem? a (cdr lat)
                                         (lambda (x) (cons (car lat) x)))))))) ;;; 漏了一个最核心的tail，无法进行函数递归
      (rem? lat))))

(rember8k 'a '(a b c d a) (lambda (x) x))


(define rember8k
  (lambda (a lat tail)
    (letrec ((rem? (lambda (lat)
                     (cond
                       ((null? lat)(tail (quote ())))
                       ((eq? (car lat) a) (tail (cdr lat)))
                       (else (rem? a (cdr lat)
                                         (lambda (x) (tail (cons (car lat) x)))))))))
      (rem? lat))))

(rember8k 'a '(a b c d a) (lambda (x) x))



(define multi-rember8k
  (lambda (a lat tail)
    (letrec ((rem? (lambda (lat tail)
                     (cond
                       ((null? lat)(tail (quote ())))
                       ((eq? (car lat) a) (rem? (cdr lat) tail)) ;; (tail x) =tail
                       (else (rem? (cdr lat)
                                   (lambda (x) (tail (cons (car lat) x)))))))))
      (rem? lat tail))))


(multi-rember8k 'a '(a b c d a) (lambda (x) x))