求定积分
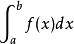
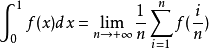
(define (cube x) (* x x x))
;;;累加
(define (sum-integer a b)
(if (> a b)
0
(+ a (sum-integer (+ a 1) b))))
(sum-integer 1 10)
;;;立方累加
(define (sum-cube a b)
(if (> a b)
0
(+ (cube a) (sum-cube (+ a 1) b))))
(sum-cube 1 3)
;;; 求Pi 值 分数累加
(define (sum-pi a b)
(if (> a b)
0
(+ (/ 1.0 (* a (+ a 2))) (sum-pi (+ a 4) b))))
(sum-pi 1 9)
观察上面的积分过程 ##最终提取出公共的形式 Sum
;; (define (<name> a b)
;; (if (> a b)
;; 0
;; (+ (<term> a) (<name> (<next>a) b))))
于是我们可以得到
(define (sum term a next b)
(if (> a b)
0
(+ (term a) (sum term (next a) next b))))
And Apply the sum to get the sum-integer2 sum-cube2 sum-pi2
(define (sum-integer2 a b) (sum (lambda (x) x) ((lambda (x) (+ x 1)) a) (lambda (x) (+ x 1)) b)) ;;;-->There is some problems
;> (sum-integer2 1 10)
;54 ------------------------>Why
;> (sum-integer 1 10)
;55
(define (identity x) x)
(define (inc x) (+ x 1))
(define (sum-integer3 a b) (sum identity a inc b))
(sum-integer3 1 3)
(define (sum-cube2 a b) (sum cube a inc b))
(sum-cube2 1 3)
(define (sum-pi2 a b)
(define (pi-term x)
(/ 1.0 (* x (+ x 2))))
(define (pi-next x)
(+ x 4))
(sum pi-term a pi-next b))
(sum-pi2 1 9)
(* 8 (sum-pi2 1 1000))
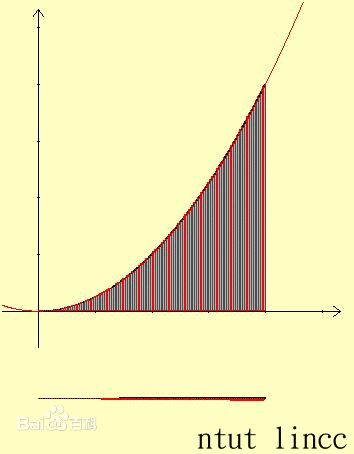
也就是我们现在可以计算积分了！
我们的问题是求解下面的定积分：
;;;; So now we can do the integrate computing
;;Because integrate will have the same function but different next function
;;;a-b 之间关于f函数的定积分的求法
(define (integral f a b dx)
(define (add-dx x) (+ x dx))
(define (update-a a dx) (+ a (/ dx 2.0)))
(* (sum f (update-a a dx) add-dx b) dx))
(integral cube 0 1 0.01)
(integral cube 0 1 0.001)
(integral cube 0 1 0.0001)
(/ 1 4.0)
(/ (* 1 (cube 1)) 4.0)
;result:
;0.24998750000000042
;0.249999875000001
;0.24999999874993412
;0.25
;0.25
为了更精确的求解积分，我们使用更为精妙的辛普森积分
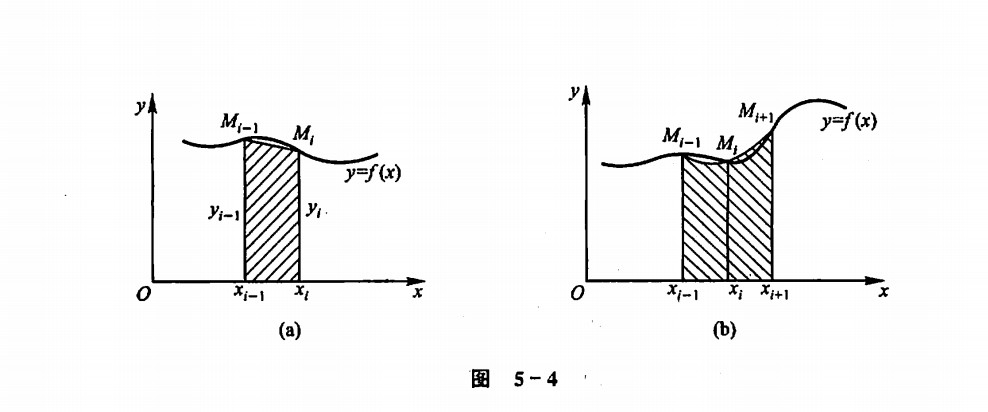
###包含奇数的两倍 和偶数的四倍，两边不加倍
- h = (b-a)/n
- yk= f(a+kh) —> next
- (even? k) (odd? k)
- y0 =a yn= b
a. 设计的过程遇到的问题是 参数的问题 需要设置k？ b. 中间过程的问题，如何划分三种情况 b.1 k为0和n的情况 b.2 k为奇数的情况 b.3 k为偶数的情况
最终, 利用Fact的思想 进行求积分
;;; 下面是一个较为混乱的设计，且没有考虑使用sum
(define (simpson-integral f a b n)
(let ((h (/ (- b a) n))
(k 0))
(define inc (+ a (* k h)))
(define inc2 (* 2 f(inc)))
(define inc4 (* 4 f(inc)))
(cond
((= k 0) (f a))
((= k n) (f b))
((even? k) (+ (* 2 f((+ a (* k h))))
)))
补充，好思想:保证最后一个为偶数
(define (round-to-next-even x)
(+ x (remainder x 2))
)
于是有了下面较好的版本，思考，之前的Sum其实是已经提供了inc递增的a 以及范围，我们主要的目的就是写好term即可！而 term其实就是涉及到你需要思考的三种情况 之前你之所以回想不清楚，因为你没有斩断念头，term只接受一个参数， 这个参数其实就是你一直想的k，所以simpson-term的一个参数就是k，利用它 开始做文章即可
(define (simpson-integral f a b n)
(define (round-to-next-even x) (+ x (remainder x 2)))
(define fixed-n (round-to-next-even n))
(define h (/ (- b a) fixed-n))
(define (simpson-term k)
(define y (f (+ a (* k h))))
(cond
((or (= k 0) (= k fixed-n))
(* 1 y))
((even? k) (* 2 y))
(else (* 4 y))))
(* (/ h 3) (sum simpson-term 0 inc fixed-n))
))
;(simpson-integral cube 0 1 10)
;1/4
另外还有几种变体，只不过总体思路都在上面类似。
a1:breaking the problem into four parts: (f y0), (f yn) and two sums,one over even k and another over odd k
(define (another-simpson-integral f a b n)
(define h (/ (- b a) n))
(define (add-2h x) (+ x (* 2 h)))
(* (/ h 3.0) (+ (f a)
(* 4.0 (sum f (+ a h) add-2h (- b h)))
(* 2.0 (sum f (add-2h a) add-2h (- b h)))
(f (+ a (* h n))))))
a2:Here’s a version that sums over pairs of terms (2 y_k + 4 y_k+1). No conditionals or special cases are needed anywhere, but there’s an extra term [f(b) - f(a)] to be added to the final count.
(define (simpson f a b n)
(define h (/ (- b a) n))
(define (y k)
(f (+ a (* k h))))
(define (ypair k)
(+ (* 2 (y k))
(* 4 (y (+ k 1)))))
(define (add-2 k)
(+ k 2))
(* (/ h 3) (+ (sum ypair 0 add-2 (- n 1))
(- (f b) (f a)))))
当然也可以写成下面的格式：
(define (sim-integral f a b n)
(define h (/ (- a b) n))
(define (y k) (f (+ a (* k h))))
(define (coeff k) (if (is-even? k) 2 4))
(define (part-term k) (* (coeff k) (y k)))
(define part-value (sum part-term 1 inc (- n 1)))
(* (/ h 3) (+ (y 0) (y n) part-value)))
##下面是我重新写的一遍，包含一些计算问题的修正
- 加入了n的修正
- 重新认识了simpson算法的，当然还有些问题没有理解，比如f(b)-f(a), 在simpson-anthother-integrate中
新的源码如下:
;;; (let <var> <bindings> <body>)
(define (cube x) (* x x x))
(define (sum-integer a b)
(if (> a b)
0
(+ a (sum-integer (+ a 1) b))))
(sum-integer 1 10)
(define (sum-cube a b)
(if (> a b)
0
(+ (cube a) (sum-cube (+ a 1) b))))
(sum-cube 1 3)
(define (sum-pi a b)
(if (> a b)
0
(+ (/ 1.0 (* a (+ a 2))) (sum-pi (+ a 4) b))))
(sum-pi 1 10)
(sum-pi 1 100)
(define (sum term a next b)
(if (> a b)
0
(+ (term a) (sum term (next a) next b))))
(define (sum-integer2 a b)
(define (identity x) x)
(define (inc x) (+ x 1))
(sum identity a inc b))
(sum-integer2 1 10)
(define (sum-cube2 a b)
(define (cube x) (* x x x))
(define (inc x) (+ x 1))
(sum cube a inc b))
(sum-cube2 1 3)
(define (sum-pi2 a b)
(define (pi-term x) (/ 1.0 (* x (+ x 2))))
(define (pi-next x) (+ x 4))
(sum pi-term a pi-next b))
(sum-pi2 1 10)
(define (integral f a b dx)
(define const_a (+ a (/ dx 2.0)))
(define (add_dx x) (+ x dx))
(* (sum f const_a add_dx b) dx))
(integral cube 0 1 0.001)
(define (simpson-integral f a b n)
(define (round-to-next-even x) (+ x (remainder x 2)))
(define fixed-n (round-to-next-even n))
(define (inc x) (+ x 1))
(define h (/ (- b a) fixed-n))
(define (simpson-term k)
(define y (f (+ a (* h k))))
(cond
((or (= k 0) (= k fixed-n))
(* 1 y))
((even? k)
(* 2 y))
(else (* 4 y))))
; (* (/ h 3) (sum simpson-term 0 inc b))) ;;; 0的意思表示从k=0开始,不能写成b，如果写成b表示你没有理解，因为0 fixed-n都代表的是K
;;这是次数的说法，而不是代表着a-b之间的求值范围，而是指求职的次数！
(* (/ h 3) (sum simpson-term 0 inc fixed-n)))
(simpson-integral cube 0 1 10)
(simpson-integral cube 0 1 11)
;;一种变体 思路同上
;; 比较有趣的地方是分为四个节点出
;; 1 f(a) ----》 y0
;; 2 f(a+h) 奇数的开始地方 add-2h方式累加都是奇数 同时终点是b-h 为什么？因为b在下面被暂用--》把它看待是一个奇数累加的过程 y1 y3 y5
;; 3 f(a+2h) 偶数的开始地方 add-2h方式累加都是偶数 同时终点是b-h--》把它看待是一个偶数累加的过程 y2 y4 y6..
;; 4 f(b) 最后一部分 yn
(define (simpson-another-integral f a b n)
(define h (/ (- b a) n))
(define (add-2h x) (+ x (* 2.0 h))) ;;;
(* (/ h 3.0) (+ (f a)
(* 4.0 (sum f (+ a h) add-2h (- b h))) ;;; (+a h)表示起始点 (- b h) 表示的是终点
(* 2.0 (sum f (add-2h a) add-2h (- b h))) ;; 注意这边的(add2h a)表示的是起始点
(f (+ a (* h n)))))) ;; 也可以是(f b)
;> (simpson-another-integral cube 0 1 11)
;0.1782892789654623
;> (simpson-another-integral cube 0 1 12)
;0.2499999999999999'
(define (simpson-another-integral-improve f a b n)
(define (round-to-next-even x) (+ x (remainder x 2)))
(define fixed-n (round-to-next-even n))
(define h (/ (- b a) fixed-n))
(define (add-2h x) (+ x (* 2.0 h))) ;;;
(* (/ h 3.0) (+ (f a)
(* 4.0 (sum f (+ a h) add-2h (- b h))) ;;; (+a h)表示起始点 (- b h) 表示的是终点
(* 2.0 (sum f (add-2h a) add-2h (- b h))) ;; 注意这边的(add2h a)表示的是起始点
(f (+ a (* h fixed-n)))))) ;;; (f b)的效果是一样 但是不正确！ 现在
(simpson-another-integral cube 0 1 11)
(simpson-another-integral cube 0 1 12)
(simpson-another-integral cube 0 1 111);;; 如果是奇数的话，现在解决的办法就是多增加一些计算！
;;;;;过程没错！！！ 不知道哪边多加了！
(define (simpson-pair-integral f a b n)
(define (round-to-next-even x) (+ x (remainder x 2)))
(define fixed-n (round-to-next-even n))
(define h (/ (- b a) fixed-n))
(define (y k) ( f (+ a (* k h))))
(define (ypair k)
(+ (* 2 (y k))
(* 4 (y (+ k 1)))))
(define (add-2 k)
(+ k 2))
(* (/ h 3) (+ (sum ypair 0 add-2 (- fixed-n 1))
(- (f b) (f a))))) ;;; 为什么是减号 你可以看到这边的思想是抽出中间的偶数对的数据（奇数加上偶数 理当是加起来的)
;;;因为最后一个 为什么要计算 [f(b) - f(a)]
(simpson-pair-integral cube 1 3 1)
(simpson-pair-integral cube 1 3 2)
;;;sim-integral 提高版 加入了 round-to-next-even使得计算准确，先前的sim-integral有问题
(define (sim-integral f a b n)
(define (round-to-next-even x) (+ x (remainder x 2))) ;;;得加上这个 才可以算准！！
(define fixed-n (round-to-next-even n))
(define h (/ (- b a) fixed-n))
(define (y k) (f (+ a (* k h))))
(define (coeff k) (if (even? k) 2 4))
(define (part-term k) (* (coeff k) (y k)))
(define (inc x) (+ x 1))
(define part-value (sum part-term 1 inc (- fixed-n 1)))
(* (/ h 3) (+ (y 0) (y n) part-value)))
(sim-integral cube 1 3 10) ;;; 有问题 已解决
(sim-integral cube 1 3 11) ;;; 有问题 已解决
令狐冲
Engineer of offshore wind turbine technique research
My research interests include distributed energy, wind turbine power generation technique , Computational fluid dynamic and programmable matter.