Haskell是一门很深的(deep)语言，需要经常去考究，下面有一些渠道可以 经常去查阅类型的推理过程。

Standard Prelude包含着基本的Preude加载的模块，类，函数等，相当具体。 现在终于发现haskell的类型类其实就是抽象类或者比抽象类更抽象的接口类，通过class来定义(在java中无论是抽象类还是实体类都使用class,现在haskell区分来class定义抽象类或者接口类,date定义实体类)

必须经常去查查这些函数的实现

• Data.Char 100多个
• Data.List 200多个
• Data.Map 200多个
• Data.Set 100多个

还有其他350种以上这种类型。。。

---

一个问题：我们必须为要进行比较的不同类型使用不同名字的函数。这很低效且令人厌烦。如果能够只使用 ==

来比较任何东西将方便很多。== 在实现像 /= 这样的泛型函数也很有用，几乎对任何事物都有效。有了一个可以比较任意事物的函数，我们可以让自己的代码更通用：如果一段代码只是需要比较一些事物，它就应该可以接受任意数据类型，编译器知道如何比较它们。并且，如果后来增加了新的数据类型，已有的代码不需要进行修改。

类型类定义一组函数，这些函数依赖于所给定的数据的类型可以有不同的实现。类型类看上去可能像面向对象编程中的对象，但是它们确实很不相同。

让我们用类型类来解决本章前面的相等性测试的难题。首先，必须定义类型类本身。我们想要一个函数，它接受两个相同类型的参数并返回一个Bool值来表示两个参数是否相等。我们不关心参数的类型是什么，只是需要这种类型的两个项。这是我们的类型类的第一个定义：

— file: ch06/eqclasses.hs
class BasicEq a where
   isEqual :: a -> a -> Bool

这里声明了一个名为BasicEq的类型类，用字母a表示实例的类型。这个类型类的实例是任何实现了其中所定义的函数的类型。这个类型类定义了一个函数。这个函数取两个参数－都是这种实例的类型－并且返回一个Bool值。

Haskell的类型类被设计来做这些事情。 Haskell中定义类型类的关键字是 class。不幸的是这可能会让来自面向对象编程的人们搞混，因为我们所说的并不是一回事！ 第一行里面参数名a是任意选择的。可以用任何名字。关键点是，在函数中要列出类型时，必须用实例的名字。

• 一些数值算子：

Numeric 类型

Haskell有一组非常强大的数字类型。从快速的32位或64位整数到任意精度的有理数都可以使用。你可能已经知道了像这样的操作符可以对所有这些类型使用。这个特性是用类型类实现的。作为附加的好处，它允许你定义自己的数字类型，并把它作为Haskell中的一等公民。

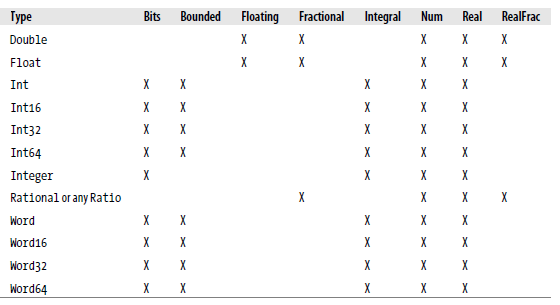
在开始讨论数字类型时，先查看下这些类型本身。表6-1 “Numeric类型精选”描述了Haskell中最常用的数字类型。注意还有些其他的数字类型可用，用来实现与C交互等特定用途。

###Table 6.1. Numeric 类型精选

这些是相当多不同的数字类型。有一些像相加这样的操作，可以用在所有这些类型上。还有其他的入 asin，只用在浮点数类型上。表6－2“Numeric函数和常量精选”里总结了操作不同数字类型的函数，表6-3 “Numeric类的类型类实例”将类型与它们相应的类型类进行匹配。在读这个表时，记住Haskell的操作符只是函数： (+) 2 3 或者 2 + 3 结果都一样。按照习惯，把操作符作为函数时，写在括号里。

###Table 6.2. “Numeric函数和常量精选”

经常需要在数字类型之间进行转换。表6-2 “”列出了很多可以用来做转换的函数。然而如何在任意两个类型间进行转换并不总是显而易见的。表6-4“在Numeric类型间转换”提供了如何在不同类型间转换的信息。

可以用 round, ceiling 或者 floor 替代 truncate。

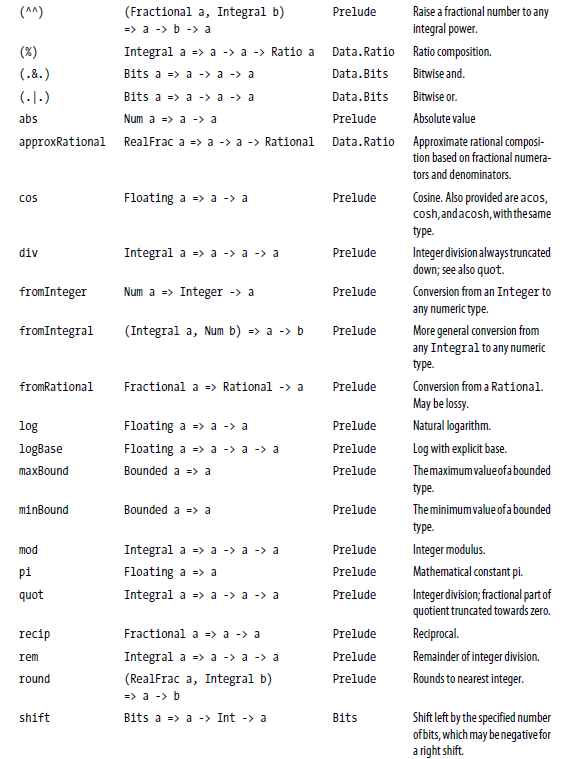
在“扩展实例：Numeric类型”一节有其他的例子演示如何使用这些数字类型类。 相等性，顺序性，及比较我们已经说过了算术操作符如 + 可以用在所有不同的数字上。但是Haskell里还有些更加广泛的操作符。最明显的当然是相等性测试： == 和 /=。这些操作符定义在 Eq 类里。

还有 >= 和 <= 这样的比较操作符。它们在 Ord 类型类中声明。它们在单独的类型类中，是因为有些类型如Handle，可以做相等性测试，但是没有办法表达特定的顺序。所有Ord的实例都可以用 Data.List.sort 来排序。

几乎所有的Haskell类型都是Eq的实例，并且大部分是Ord的实例。