递归的简单阐述
递归和迭代的区别: 递归需要调用自己 迭代不断修正自己的返回值
递归伪代码: (define factoral (lambda (x) (if (<= x 1) //1.必须有一个输出口 1 //出口值 (* x (factoral (- x 1)))
所以递归就看两个部分:1 输出口(递归终止条件) 2:循环表达式,并且一定要减减 或者++ 直到能够达到递归终止条件
进一步通过java比较递归和尾递归的执行过程:
尾递归代码:
/**
*
* @param n 计算5! 则n =5
* @param product 一般是设置为1 比如 计算5! factail1(5,1)
* @return 返回递归结果
/
public static long facttail1(int n, int product)
{
if(n<0)
{
return 0;
}
if(1 == n)
{
return product;
}
else
{
return facttail1(n-1, productn);
}
}
普通递归代码: /** * * @param n 5! 则 n = 5 * @return 返回阶乘的计算结果 / public static long facttail1(int n) { long a = 0;// 用于调试,可注释 if(n==1) { a = 1;// 用于调试,可注释 return 1; } a =nfacttail1(n-1); // 用于调试,可注释 return n*facttail1(n-1); }
无递归的阶乘: /** * * @param n 计算 5! 则n=5 * @return / public static int fact2(int n) { if(n < 0) { throw new IllegalArgumentException(); } int result = 1; for(int i = 1; i <= n; i++) { result = resulti; } return result; }
主程序: public static void main(String[] args) { // TODO 自动生成的方法存根 long Apple =facttail(5,1); System.out.println(“Apple get by 尾递归:"+Apple); long Banana =facttail1(5); System.out.println(“Banana get by 递归:"+Banana); }
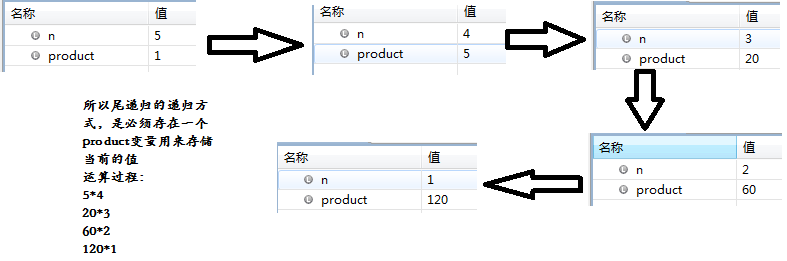
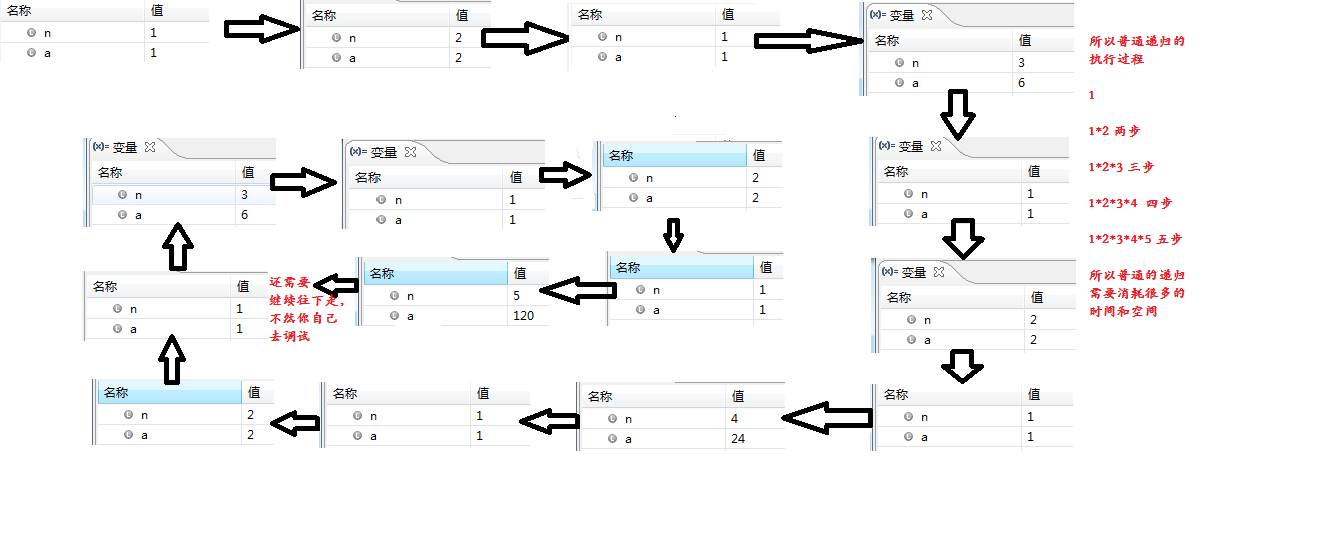
通过调试可以看到,尾递归的执行过程为: 看下图 尾递归的调试过程 而普通的递归方式为: 看下图 [size=14.4444446563721px]普通的递归运行方式
通过上述调试发现,尾递归的确是比较快的。
另外不知道java中的大的数值范围该如何表示,比如 [size=14.4444446563721px]facttail(32,1); 就运行不出来结果? long无法解决问题。估计java不适合进行大型的数值运算
利用BigInteger类型的改造版本:
import java.math.BigInteger;
/**
* @author 叶昭良
*
*/
public class TestRecursive
{
public static void main(String[] args)
{
// TODO 自动生成的方法存根
BigInteger Apple =fact(100l,BigInteger.valueOf(1));
System.out.println("Apple get by 尾递归:"+Apple);
BigInteger Banana =facttail(100l);
System.out.println("Banana get by 递归:"+Banana);
}
// 尾递归方式
/**
*
* @param n 待计算的阶乘 比如5! 则n=5
* @param product 中间变量
* @return 一个BigInteger对象,包含阶乘的计算结果
*/
public static BigInteger fact(long n, BigInteger product)
{
if(n<0)
{
return BigInteger.valueOf(0);
}
else if(n==1)
return product;
else
return fact(n-1,product.multiply(BigInteger.valueOf(n)));
}
//递归方式
/**
*
* @param n 待计算的阶乘 比如5! 则n=5
* @return 一个BigInteger对象,包含阶乘的计算结果
*/
public static BigInteger facttail(long n)
{
if(n==1)
{
return BigInteger.valueOf(1);
}else
{
//a =n*facttail1(n-1);
return facttail(n-1).multiply(BigInteger.valueOf(n));
}
}
}
运行结果:
Apple get by 尾递归:93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000 Banana get by 递归:93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
真的是可以要有多大就有多大。 java 在eclipse使用ctrl+o 调用multiply发现他需要传递一个BigInteger对象。 [c#版本 BigInteger:][https://msdn.microsoft.com/zh-cn/library/system.numerics.biginteger.aspx]
补充杨老师串讲的内容,补上参数说明,并归结为方法,进行独立测试
import java.util.Arrays;
/**
* @author 叶昭良
*
*/
public abstract class TestChuangjian2
{
/**
* @param args
*/
public static void main(String[] args)
{
// TODO 自动生成的方法存根
//第一部分 递归
// case1讲故事
tellStory(1);
System.out.println(fact(5));
System.out.println(fact2(5));
System.out.println(fact3(5,1));
System.out.println("fibnacii1 :"+fib1(5));
System.out.println(fib2(5));
System.out.println(fib3(5));
}
//第一部分 递归
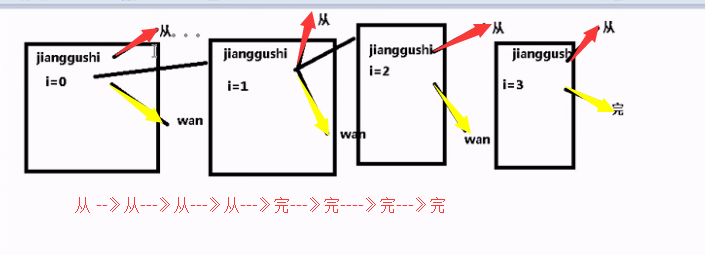
//case 1*讲故事
/**
*
* @param i 讲故事的次数
*/
public static void tellStory(int i)
{
System.out.println("从前有座山,山里有座庙,。。。。");
if(i < 3)
{
tellStory(++i);
}
System.out.println("完了");
}
//case2 阶乘
/**
*
* @param n 计算 5! 则n=5
* @return 返回阶乘的计算结果
*/
public static int fact(int n)
{
if(n < 0)
{
throw new IllegalArgumentException();
}
if( 1 == n)
{
return 1;
}else
{
return n*fact(n-1);
}
}
// case3 无递归的阶乘
/**
*
* @param n 计算 5! 则n=5
* @return
*/
public static int fact2(int n)
{
if(n < 0)
{
throw new IllegalArgumentException();
}
int result = 1;
for(int i = 1; i <= n; i++)
{
result = result*i;
}
return result;
}
// case 4 尾递归方式
/**
*
* @param n 计算 5! 则n=5
* @param result 存储阶乘的计算结果,并作为中间变量
* @return 返回阶乘计算结果
*/
public static int fact3(int n, int result)
{
if(n <= 0)
{
throw new IllegalArgumentException("胡算的阶乘数<=0");
}
if(1== n)
{
return result;
}else
{
return fact3(n-1,result*n);
}
}
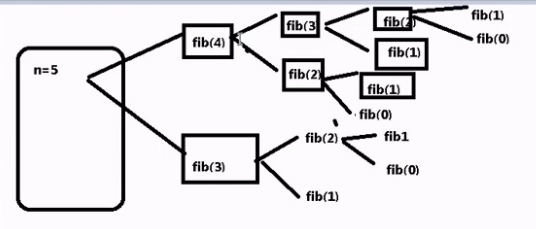
//case 5 Fibnacci1
/**
*
* @param n fibnacci的个数n
* @return fibnacci数
*/
public static int fib1(int n)
{
if(n < 0)
{
throw new IllegalArgumentException("n不可以小于0");
}
if(1 == n || 2 == n)
{
return 1;
}
else
{
return fib1(n-1)+fib1(n-2);
}
}
/**
*
* @param n fibnacci的计算数
* @return fibanacci数
*/
public static int fib2(int n)
{
int[] nums = new int[n+1];
nums[0] = 1;
nums[1] = 1;
System.out.println(Arrays.toString(nums));
for(int i = 2; i < n ; i++)
{
nums[i] = nums[i-1]+ nums[i-2];
System.out.println(Arrays.toString(nums));
}
return nums[n-1];
}
/**
*
* @param n fibnacci的计算数
* @return fibanacci数
*/
public static int fib3(int n)
{
int apple = 1;
int banana = 1;
int temp = 1;
for (int i = 2 ; i < n; i++)
{
temp = apple + banana;
banana = apple;
apple = temp;
}
return temp;
}
}
一个反例:栈溢出 stackOverFlowError 一般要求的StackSize是1MB
反例:
/**
*
* @param i 讲故事的次数
*/
public static void tellStory(int i)
{
System.out.println("从前有座山,山里有座庙.....");
{
tellStory(++i); // i+1
}
System.out.println("Time Over in "+i);
}
运行完之后会报错,问题原因是栈溢出,达到栈的最大容量限制。 结论:在递归中必须设置终止条件,这样才不至于引起栈溢出。